Machine Learning basics and Naive Bayes Classifier

Introduction

As I learnt from one of the Microsoft’s learning resource, machine learning answers mostly just five types of questions:

1. Is this A or B (Classification Problem)
2. How much?  (Regression Problem)
3. How is this organized? (Clustering Problem)
4. Is this weird?   (Anomaly Detection)
5. What’s next?    (Reinforcement learning)

We use use various algorithms and techniques to answer these questions. Machine learning is broadly classified in Supervised, Unsupervised, Deep-learning and Reinforcement learning.

Supervised learning: When we have labled data avaliable for applying machine learning techniques.

UnSupervised learning: When we do not have labled data avaliable for applying machine learning techniques.

Deep learning: This is a highly evolved branch of machine learning, where a model itself identifies the best features for the model with very less manual efforts and provide very high accuracies. Best to be used for image or sound data.

Reinforcement Learning: This area of machine learning is about taking suitable action to maximize reward in a particular situation, it i s employed by various software and machines to find the best possible behaviour or path it should take in a specific situation.

In this blog, I will dive deep in Naive Bayes Classifier, which is one of the most popular technique for classification problems in machine learning.

Naive Bayes Classifier

Naive bayes algorithim is derivied from the famous Baye’s theoram of probability.

Baye’s theoram of probability

 Conditional Probability is basically trying to find a probability of an event based on a condition given or assumed. Notation for Conditional Probability is as follows:

P (A|B): This should be read as, probability of event A; given that event B already happened.

                         provided P (B) >0

 

Bayes’ theorem have subtle difference than Conditional Probability. In a nutshell, it gives you the actual probability of an event given information about tests.. Now its important to understand the terms Events and Tests, with respect to Probability.

• Events : “Events” Are different from “tests.” For example, there is a test for liver disease, but that’s separate from the event of actually having liver disease.
• Tests: Tests are flawed: just because you have a positive test does not mean you actually have the disease. Many tests have a high false positive rate. Rare events tend to have higher false positive rates than more common events. We’re not just talking about medical tests here. For example, spam filtering can have high false positive rates. Bayes’ theorem takes the test results and calculates your real probability that the test has identified the event.

Lets drive Baye’s Theoram: 

This is the fourmala for Baye’s Theoram. Let’s understand what probability each part of the equation denotes.

Posterior Probability:  Posterior probability is the probability an event will happen after all evidence or background information has been taken into account.

Likelihood:  Probability is about a finite set of possible outcomes, given a probability. Likelihood is about an infinite set of possible probabilities, given an outcome.

Prior Probability:  Prior probability, in Bayesian statistical inference, is the probability of an event before new data is collected. This is the best rational assessment of the probability of an outcome based on the current knowledge before an experiment is performed.

Marginal Probability:  Marginal probability is the probability of an event irrespective of the outcome of another variable.

Naive Baye’s Classifier

As name suggests Naive Baye’s Classifier is used for Classification Problems, example : For a given problem statement answer is either TRUE or FLASE, whichever outcome will have higher probability will be our final outcome or final decision.

Let’s understand with the help of example, 

Problem Statement: Is it a good day to play golf?

What we have in hand?  Past data, that tells on whar kind of whether conditions golf was played.

In table above (which is our dataset) columns Outlook, temperature, Humidity, Windy are the features for the dataset and will be representated as dataset X and it have features {x1,x2,x3……..xn} and  column Play Golf is the outcome and will represented as Class variable  {y} with possible outcomes Yes/No.

The datset can be read as : A Rainy, Hot and highly humid day is not good to play Golf and also a Sunny, Cool, Normal Humid and non windy day is good to play golf. 

Based on our dataset the Baye’s Theoram can be re-written as :

                                       

Now as we know, X  have features {x1,x2,x3……..xn}, we can replace the dataset X with features as below: 

                                           

As the denominator remains constant the above equation can be rewritten as:

                                               

Now as I mentioned in my first statement in Naive Baye’s which ever class will have highest probability will be the outcome, so we can simply fetch maximum probability using argmax function on y:

                   

And this is how a Classification problem is solved using Naive Baye’s Classifier.

 

 

Probability for Machine learning

Probability is the basic we must know for Machine learning and to begin with I believe ‘Random Variable’ is the best to start with.

In this blog, you may notice few topics are just introduced and are not explained end to end, that’s because I am trying to cover topics that matter more in Machine learning perspective.

What is a Random Variable?

As per the definition by “Google” :

“A random variable is a variable whose value is unknown, or a function that assigns values to each of an experiment’s outcomes.”

Sounds Hard? Let me try to explain better.

What if I say, A random variable is any one possible outcome of the experiment that we are performing. For example: A Dice that have six sides {1,2,3,4,5,6} can get any of these 6 numbers when I roll it, in other words, I can say that ‘X’ is a random variable that can take any value from {1,2,3,4,5,6} when a dice is rolled. Please note that ‘X’ is a variable that can hold ‘1’ value its not an array or list.

Types of Random Variable

To make it simple there are two categories of a random variable

1. Discrete Random Variable
2. Continuous Random Variable

Discrete Random Variable

When you have a range very well defined and from that range there can be one outcome then it is a discrete random variable. What does that mean? Let’s go back to the dice example, the only and only possible outcomes are {1,2,3,4,5,6} and we can’t get 4.5 in our experiment of rolling one dice. Then X is a discrete random variable. Few more examples of discrete random variables are:

1. A bag full of balls
2. Levels of a game
3. Number of chocolates in a chocolate box.

Continuous Random Variable

When an event do not have a very well defined range, or in other words we can say, there is a dense range for e.g. [4,5] have a countibily infine range between 4 and 5, and from that range there can be one outcome then it is a continuous random variable.

What does that mean?  When you are trying to estimate/guess (not calculate) a height of person, then, can you be accurate to the 10 decimal places? Certainly, not. That means even if you are extremely close to say that person is nearly 162 cm, there is a chance of at least 10^th decimal place it is less or more, which means we do not have a straight forward range. This is an example of Continuous Random Variable Few more examples of Continuous random variable are:

1. Weight of entity
2. Speed of a vehicle
3. Timestamps

Permutations and Combinations for Probability

Probability and Permutations & Combinations go hand in hand, so we must take a quick look at the permutations & Combinations formula before we go ahead,

What is permutation and combinations?

If I am tossing a coin 3 times, then how many “combinations” of output I may get, let’s take a look:

As displayed above, for a simple coin, tossed 3 thrice, there are 8 combinations of output that are possible.

To be noted here, when we are trying to find all the possible outcomes then order of head and tails does matter and we can simply calculate this by using a logic

2 outcomes in each flip, so for three flips => 2*2*2 = 8 or simply 2³ 

Now suppose, I need to know out of total outcomes how may will have exactly 2 tails.

Then, each outcome comprises of 3 values ‘HHH’ for example and we want to know how many ways two tails can be arranged and how many ways 1 head can be arranged in this set of three values. We have a simple formula to calculate this

where n is the number of values in a set, r is the number desired output. For our example we have a set of three so n = 3 and we want to arrange 2 tails so r = 2.

 

Which results in 3 and we can verify the same using our toss chart.

For our current goal, we do not need to dive deep into Permutations & Combinations and knowing the formula and how to solve it would suffice. I will take this example forward to explain probability.

Probability:

The chance of an event to occur in the given number of trials is called probability.

By this I mean if I want my dice to throw 5 for me, then the chances I will get 5 are 1/6.

How? Total numbers of outcomes a die may have are 6 so my sample size is 6 {1,2,3,4,5,6} and I want just 1 number from it (my choice is 5, it could be ‘4’ or ‘3’ or any number within {1,2,3,4,5,6})

So, Probability = Desired outcome/ Total number of possible outcomes

It’s not always that straight forward and this is the most basic example I gave.

Lets go back to coin toss example and calculate the probability of getting exactly two tails when a coin is flipped thrice

As we have already saw from our calculations in permutaions & combinations sections we know that,

Total outcomes possible are 8 and out of which 3 times its possible to get exactly 2 tails.  So our probability would be 3/8.

Now lets look at few interesting concepts on which probability highly depends.

Independent, Dependent and Mutually Exclusive trials:

Suppose my problem statement says: “From a bag full of 5 blue and 6 red balls, what is the chance/probability of getting exactly blue ball in each of the 3 trails while drawing one ball at a time”

Dependent trials:

 

Dependent trials are the ones when the outcome of one trial impacts the probability of other trail.  In problem stated above, if, I am checking the color of the ball and not re-placing it back in bag, rather keeping it aside then the total number of balls are changing for each following trail and hence impacting their probabilities.

Independent trials:

If in each trial I am checking the color of the ball and putting it back in bag, then my total number of balls in bags remains same for each trail and probability of getting a blue ball will remain same in all the trails. So I can say, “The outcome of one trial is independent of the other trial”

Mutually Exclusive trials:

If I roll a die then, on one outcome I can’t get 2 values together. I can either get 1 or 2 or 3 etc. or all of them are mutually exclusive and have nothing to do with each other. Such events are Mutually exclusive events/trials.

Conditional Probability:

Another very important concept in probability is Conditional Probability, which is basically trying to find a probability of an event based on a condition given or assumed. Notation for Conditional Probability is as follows:

P (A|B): This should be read as, probability of event A; given that event B already happened.

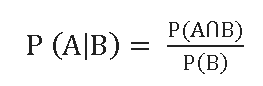                         provided P (B) >0

It is best to understand Conditional probability through example, so that we understamd the concept rather than learning definition.

Rolling a dice again: As we saw above, the sample size for a dice is {1,2,3,4,5,6} and probability of getting 3

Now if I say:

Given an odd number is rolled what is the probability of getting 3?

In this case our reduced sample size is {1,3,5} and probability of getting a 3 now

This probability we derived using basic probability logic, we can get the same using formula stated above

Entire sample size: {1,2,3,4,5,6}

Let getting 3 in entire sample size is Event A = {3}

and all odds is Event B = {1,3,5}

Then, probability of A and B both happening is  which is getting probability of A and B both happening in entire sample size and that just once that is ‘3’, so

And probability of event B in entire sample space.

Hence, by Conditional probability formula:

 This example is taken from Sir Jeremy Balka’s statistics lectures. Thanks to him for amazing content to grasp this concept with such ease.

Probability Distributions:

As the name suggests, it shows for an event how the probability is distributed for a certain range of values.

For both the types for random variables there are probability distributions:

1. Discrete Probability distributions
2. Random Probability distributions

Discrete Probability distributions

Probability distribution for a discrete random variable, as discrete random variables have jump in numbers and hence the probability distribution is represented by a histogram.

Discrete Probability distributions characterized into various kinds, few are listed as below.

1. Binomial Distribution: We apply Binomial distribution when we are trying to find the number of success in ‘N’ INDEPENDENT trails
2. Hyper-Geometric Distribution: We apply Hyper-Geometric distribution when we are trying to find the number of success in ‘N’ DEPENDENT trails
3. Geometric Distribution: This is used when we try for find the 1^st success in ‘N’ independent trials.
4. Negative Binomial Distribution: This is used when we try for find the n^th success in ‘N’ independent trials.

Continuous probability distributions:

Probability distribution for a continuous random variable, as continuous random variables have dense bunch of values e.g. within [4, 5] there is a big range of numbers (often called countably infinite) and hence the probability distribution is represented by a curve (Bell shaped curve).

Continuous Probability distributions characterized into various kinds, few are listed as below.

1. Normal distribution
2. Log-Normal distribution
3. Pareto distribution

Continuous probability distributions are extremly important in Machine learning and its unfair to put one-liners for them hence, I will discuss these in detail in another blog.

Naive Bayes Classifier in Machine Learning:

Now that we know probability and conditional probability, lets understand a very important machine learning algorithm Naive Bayes Classification Algorithm.